Previously … on Machine Learning here
From my blog on Artificial Intelligence (AI), we know that when it comes to processing data and creating patterns for decision making, the aim is to imitate the workings of the human brain. Deep learning (DL) is a subset of Machine Learning (ML) and AI. It has neural networks which are capable of learning unsupervised from data that is unstructured or unlabeled.
In the digital era, we are getting information from everywhere. Big Data is found from sources such as social media, internet search engines, online platforms etc. Big Data is accessible and is shared through FinTech applications such as cloud computing. However, this data is unstructured, and so huge that it would take you and me years to understand and get the relevant information from it. There is boundless potential in decoding Big Data, so companies are using AI techniques to do this.
A common techniques to process Big Data is ML. ML uses self-adapting algorithms to get better at analysis and find patterns with experience or additional data. More information on ML can be found in my previous blog article.
Deep learning, a subset of machine learning, utilizes a hierarchical level of Artificial Neural Networks (ANN) to carry out the process of machine learning. To understand how Deep Learning Works, we must first understand ANN.
Artificial Neural Networks (ANN)
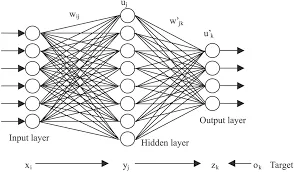
In DL, the computing systems are designed to simulate how the human brain analyzes and processes information. ANN has self-learning capabilities that allow it to produce positively correlated results with the amount of available information.
How does ANN work?
Artificial neural networks are built like the human brain, with neuron nodes interconnected like a web. The human brain has hundreds of billions of cells called neurons. Each neuron is made up of a cell body that is responsible for processing information by carrying information towards (inputs) and away (outputs) from the brain. ANN has hundreds or thousands of artificial neurons called processing units which are interconnected by nodes.
These processing units are made up of input and output units. The input units receive various forms and structures of information. The neural network attempts to learn about the information presented in order to produce one output report. Just like humans need rules and guidelines to come up with a result or output, ANNs also use a set of learning rules called Backpropagation to perfect their output results.
An ANN goes through a training phase where it learns to recognize patterns in data. During this supervised phase, the network compares its actual output produced with the desired output. The difference between both outcomes is adjusted using backpropagation. At this stage, the network works backwards, going from the output unit, through the hidden units to the input units in order to adjust the weight of its connections between the units. It iterates until the difference between the actual and desired outcome produces the lowest possible error.

During the training and supervisory stage, the ANN is taught what to look for and what its output should be, using Yes/No questions with binary numbers. For example, a bank that wants to detect credit card fraud on time may have four input units fed with these questions:
-
Is the transaction in a different country from the user’s resident country?
-
Is the website the card is being used at affiliated with companies or countries on the bank’s watch list?
-
Is the transaction amount larger than $2000?
-
Is the name on the transaction bill the same as the name of the cardholder?
The bank wants the “fraud detected” responses to be Yes Yes Yes No which in binary format would be 1 1 1 0. If the network’s actual output is 1 0 1 0, it adjusts its results until it delivers an output that coincides with 1 1 1 0. After training, the computer system can alert the bank of pending fraudulent transactions, saving the bank money.
ANN Application to Deep Learning
While traditional programs build analysis with data in a linear way, the hierarchical function of deep learning systems enables machines to process data with a non-linear approach. A traditional approach to detecting fraud or money laundering might rely on the amount of transaction that ensues, while a deep learning non-linear technique to weeding out a fraudulent transaction would include time, geographic location, IP address, type of retailer, and any other feature that is likely to make up a fraudulent activity.
The first layer of the neural network processes, is raw data input, such as the amount of the transaction. This is then passed on to the next layer as output. The second layer processes the previous layer’s information by including additional information like the user’s IP address and passes on its result. The next layer takes the second layer’s information and includes raw data like geographic location and makes the machine’s pattern even better. This continues across all levels of the neuron network until the best output is determined. This is an example of a FeedForward Neural Network.

warning Little Bit of Maths on the Horizon! The next section is here purely for higher understanding of neural networks. If Maths is something you left in your dust at school, simply skip forward to Examples. (Click on the Equations for a GIF(t) to help you along!)
Sigmoid Neuron
In ANN we mention weights of neurons. These weighted neurons are called Sigmoid Neurons. Some neural networks use perceptron outputs that have discrete values of 0 and 1. A sigmoid neuron outputs a smooth continuous range of values between 0 and 1. This is defined by the Sigmoid Function defined below,
In ANN, values change very slowly with each iteration and input. Observing how a small change in the bias value or the weights (associated with the artificial neurons) affects the overall value of the output of the the neuron is very important. A Perceptron may have its outputs flipped suddenly with a small change in the input value. To observe the tiny changes in the output to arrive at the correct value of input, we need a function to be applied on the dot product of weights and bias value so that overall output is smooth. For now, the function could have been any function f() that is smooth in nature, such as quadratic functions or cubic functions. The reason the sigmoid function is chosen, is that, exponential functions generally are similar to handle mathematically and, since learning algorithms involve lots of differentiation, choosing a function that is computationally cheaper to handle is wise.
The Sigmoid Neurons are organized into layers, similar to how they are in the human brain. Neurons on the bottom layer (inputs) receive signals from the inputs, where neurons in the top layers (outputs) have their outlets connected to the “answer,” Usually there are no connections between neurons in the same layer. This is an optional restriction, more complex connectivity’s require more involved mathematical analysis. This is a feed-forward network so there are no connections that lead from a neuron in a higher layer to a neuron in a lower layer. Alternatively, there are Recursive Neural Networks (RNN). Again, these are much more complicated to analyze and train.
BackPropagation
A fundamental idea of DL and ANN is BackPropagation. We have briefly touched on backpropagation in previous blog articles but we will dive into the Algorithm into more detail.
The idea behind backpropagation is that we don’t know what the hidden units (the neurons between the input and output) should be doing, but we do know how fast the error between the iteration and actual result changes as we change the hidden activity. We want to find the steepest path from our starting results to the actual result.
Each hidden unit can affect many different output units. We start by looking at the error derivatives for one layer of hidden units. Once we have the error derivatives for one layer of hidden units, we use them to compute the error derivatives for the activities of the layer below. Once we find the error derivatives for the activities of the hidden units, it’s relatively easy to get the error derivatives for the weights leading into a hidden unit.
The symbol “y” will refer to the activity of a neuron. The symbol “z” will refer to the logic of a neuron. We start by looking at the base case of the dynamic programming problem, the error function derivatives at the output layer:
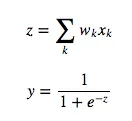
For the inductive step, let’s presume we have the error derivatives for layer j. We now aim to calculate the error derivatives for the layer below it, layer i. To do so, we must accumulate information for how the output of a neuron in layer i affects the logic of every neuron in layer j. The partial derivative of the logic, with respect to the incoming output data from the layer beneath, is merely the weight of the connection wij:
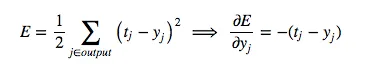
To complete the inductive step
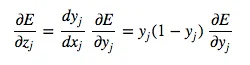
Combining, we express the partial derivatives of layer i in terms of the partial derivatives of layer j.
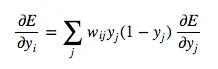
Next, we determine how the error changes with respect to the weights. This gives us how to modify the weights after each training example:
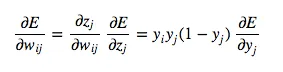
For backpropagation with training examples, we sum up the partial derivatives over all training examples. This gives us the following modification formula:
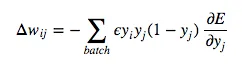
This is the Backpropagation Algorithm for Feed-Foward Neural Networks using Sigmoidal Neurons. In better news, this also the end of the Maths. You made it through, and I’m sure you’re a stronger person for it!
You can find a worked example of BackPropagation here.
Examples Of Deep Learning:

-
Email service providers use ANN to detect and delete spam from a user’s inbox
-
Asset managers use it to forecast the direction of a company’s stock
-
Credit rating firms use it to improve their credit scoring methods
-
E-commerce platforms use it to personalize recommendations to their audience
-
Chatbots are developed with ANN for natural language processing
-
Deep learning algorithms use ANN to predict the likelihood of an event
-
Colorization of Black and White Images
-
Adding Sound to Silent Movies (Charlie Chaplain will never be the same)
-
Automation of:
-
Translation of Text
-
Handwriting Generation
-
Text Generation
-
Image Captions
-
Future
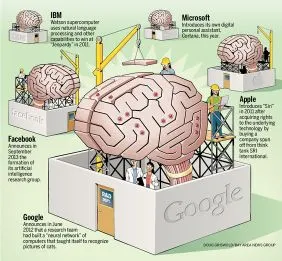
The possibilities for the future of Deep Learning are endless. As algorithms and technology advances, we may see models that use less training cases to learn, maybe diving into unsupervised learning. This could kick start a race between global companies. Apple has recently been on a hiring mission, seeking 80-plus AI experts to help make Siri smarter than Google Now or Microsoft’s Cortana. Google paid $400 million for DeepMind who specialised in Deep Learning, with Deep Learning experts commanding seven-figure salaries. They are the Premier League Footballers of the programming world.
There’s a simple reason why, when it comes to Deep Learning and AI, Google are one of, if not the, market leaders. Data! They have it coming out of their ears. We have seen that the more training cases you have for your model, the better it becomes at predictions. Apple, in this scenario, are hamstrung by their own privacy policies. As an iPhone encrypts and holds data on the device itself, Apple has little user data to exploit. A former Apple employee told Reuters that Siri retains user data for six months, but Apple Maps user data can be gone in as little as 15 minutes. This pales in comparison to the amount of data that Google aggregates from Android users around the globe. Potentially, this disparity may stifle Apple advances in AI-driven technology, and especially where big data is essential to refine and perfect the learning process.
Eventually we may see Neural networks running on our mobile devices. Mobile device may have the ability to conduct machine learning tasks locally, opening up a wide range of opportunities for object recognition, speech, face detection, and other innovations for mobile platforms.








